Numerical Analysis of a Mixed Finite Element Method for the Boussinesq Problem with Temperature-Dependent Viscosity es el nombre de la tesis que este lunes 28 de agosto presentó Javier Almonacid Paredes y que le valió obtener el título profesional de Ingeniero Civil Matemático, de la Universidad de Concepción, UdeC.

El estudio realizado por el ahora ingeniero contó con la dirección de los investigadores del Centro de Investigación en Ingeniería Matemática, CI²MA, de la UdeC, Gabriel Gatica y Ricardo Oyarzúa, quienes, a su vez, son académicos del Departamento de Ingeniería Matemática de la UdeC y del Departamento de Matemática de la Universidad del Bío-Bío, UBB, respectivamente. Este trabajo está enfocado en el análisis de un método de elementos finitos mixtos para una clase de problemas de convección natural en dos dimensiones. Más precisamente, se considera un sistema basado en el acoplamiento de las ecuaciones de conservación de momento (Navier-Stokes), masa y energía térmica por medio de la aproximación de Boussinesq (llamado problema de Boussinesq), en donde también se toma en cuenta una dependencia de la viscosidad del fluido respecto de la temperatura. Además de los profesores guia, la comisión examinadora estuvo integrada por los investigadores Eligio Colmenares de la UBB y Ricardo Ruiz-Baier del Mathematical Institute de la Universidad de Oxford, quienes evaluaron la tesis de Javier con la nota maxima.

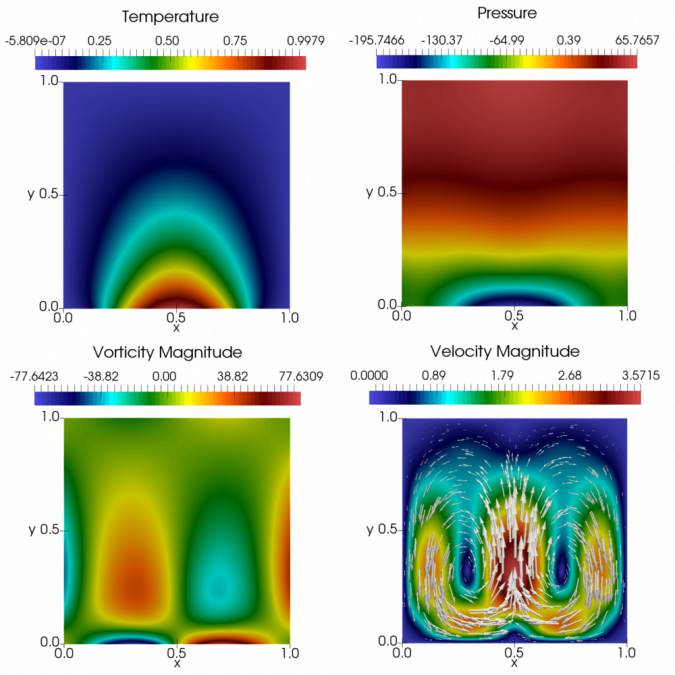
“La construcción de este método de elementos finitos comienza con la introducción de los tensores de pseudo-esfuerzo y vorticidad, y una formulación mixta para las ecuaciones de momento, la que se aumenta con términos del tipo Galerkin, con el fin de tratar la no linealidad de estas ecuaciones y el término convectivo en la ecuación de energía, para la que se considera una formulación primal”, explica Almonacid y agrega que “la temperatura prescrita en la frontera se convierte en una condición esencial, la que se impone débilmente, y que lleva a la definición del flujo normal de calor a través de la frontera como un multiplicador de Lagrange. Se puede ver que este problema altamente acoplado puede ser desacoplado y analizado como un problema de punto fijo, en donde los teoremas de Banach y Brouwer servirán para proveer de condiciones suficientes que permitan probar la buena postura de los problemas que surgen de las formulaciones continua y discreta, junto con varias aplicaciones de inyecciones continuas garantizadas por los teoremas de inyección de Rellich-Kondrachov y Sobolev. Finalmente, se presentan algunos resultados numéricos que permiten ilustrar el desempeño de este método de elementos finitos, además de probar las tasas de convergencia asociadas”.  Su tesis dio origen a una Pre-Publicacion del CI²MA, la cual ha sido enviada a publicacion a una revista de Analisis Numerico.

En cuanto a sus planes, Javier detalla que espera poder realizar una doctorado en el extranjero a partir de 2018, y dedicar lo que queda de este año, a seguir trabajando con los investigadores que guiaron su tesis, de quienes se manifiesta muy agradecido. “Con el Profesor Gatica trabajé un año completo, desde agosto de 2016 y primero desarrollamos la teoría del problema, para posteriormente empezar a trabajar en la parte numérica con el Profesor Oyarzúa durante todo el primer semestre de este año, hasta rendir el examen”, destaca. “Ahora, podemos seguir trabajando en las líneas de investigación del mismo trabajo que hicimos, porque hay muchas extensiones que podemos tomar durante los próximos meses. Pueden ser generalizaciones del problema y, por otro lado, se puede usar otros enfoques para el problema, que es algo que el Profesor Gatica ya está haciendo, por ejemplo, con Eligio Colmenares. Son temas relacionados con lo que estudiamos en mi tesis y que podríamos extender”.