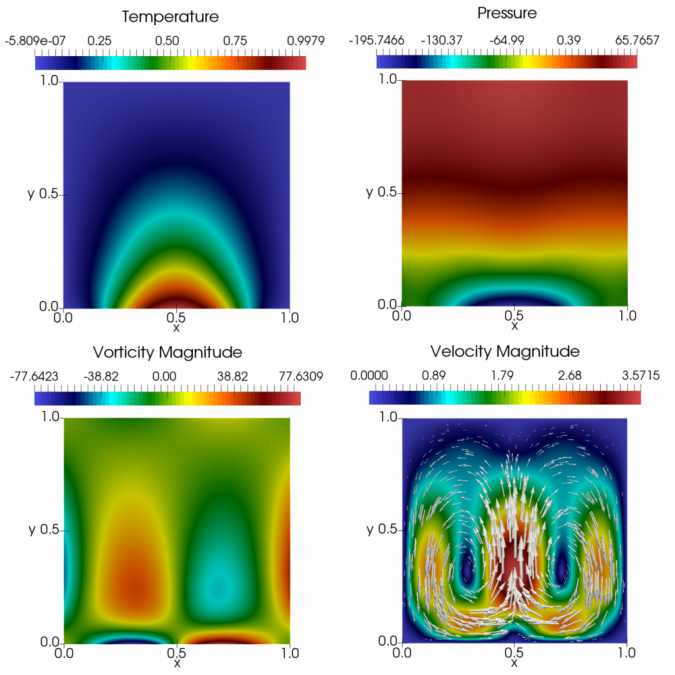
Numerical Analysis of a Mixed Finite Element for the Boussinesq Problem with Temperature-Dependent Viscosity is the name of the thesis presented on Monday 28 August by Javier Almonacid Paredes and that earned him the professional title of Mathematical Civil Engineer, University of Concepción, UdeC.

The study carried out by the now engineer was directed by researchers from Center for Research in Mathematical Engineering, CI²MA, UdeC, Gabriel Gatica and Ricardo Oyarzúa, who, in turn, are academicians of Department of Mathematical Engineering of UdeC and Department of Mathematics of Universidad del Bío-Bío, UBB, respectively. This work is focused on the analysis of a mixed finite element method for a class of natural convection problems in two dimensions. More precisely, a system based on the coupling of the steady-state equations of momentum (Navier-Stokes), mass and thermal energy conservation by means of the Boussinesq approximation (coined the Boussinesq problem) is considered, where it is also taken into account a temperature dependence of the viscosity of the fluid. In addition to the thesis advisors, the examining committee was composed by researchers Eligio Colmenares from the UBB and Ricardo Ruiz-Baier from the Mathematical Institute of the University of Oxford, who evaluated the thesis of Javier with the highest grade.

“The construction of this finite element method begins with the introduction of the pseudostress and vorticity tensors, and a mixed formulation for the momentum equations, which is augmented with Galerkin-type terms, in order to deal with the non-linearity of these equations and the convective term in the energy equation, where a primal formulation is considered”, Almonacid explains and adds the “the prescribed temperature on the boundary becomes an essential condition, which is weakly imposed, leading to the definition of the normal heat flux through the boundary as a Lagrange multiplier. It can be seen that this highly coupled problem can be uncoupled and analysed as a fixed-point problem, where Banach and Brouwer theorems will serve to provide sufficient conditions to ensure well-posedness of the problems arising from the continuous and discrete formulations, along with several applications of continuous injections guaranteed by the Rellich-Kondrachov and Sobolev embedding theorems. Finally, some numerical results are shown to illustrate the performance of this finite element method, as well as to prove the associated rates of convergence”. His thesis gave rise to a Preprint of CI²MA, which has been submitted for publication to a journal on Numerical Analysis.

As for his plans, Javier said that he hopes to be able to do a doctorate abroad beginning in 2018, and to dedicate what is left of this year, to continue working with the researchers who guided his thesis, of who he expresses gratitude. “I worked a full year with Professor Gatica, since August 2016, and first we developed the theory of the problem, for later start working on the numerical part with Professor Oyarzúa throughout the first semester of this year, until I take the exam”, he highlights. “Now, we can continue working on the research lines of the work we already did, because there are many extensions we can take over the next few months. It can be, some generalizations of the problem and, on the other hand, diverse approaches can be used to the problem, which is something that Professor Gatica is already working on with, for example, Eligio Colmenares. These are topics that are related to what we studied in my thesis and that we could extend”.