Numerical Analysis of Partial Differential Equations
Numerical Analysis is one of the few branches that are present in almost all areas of Applied Mathematics. Indeed, the benefits of Numerical Analysis have an impact in many areas of Mathematics and the Applied Sciences, such as engineering, physics, and the public and private sectors (mining industry, ecology, health sector, pulp and paper industry, education). The Research Group in Numerical Analysis of Partial Differential Equations of CI²MA, currently formed by 13 researchers, focuses on the mathematical and numerical analysis of several linear and nonlinear boundary and initial value problems appearing in physics and engineering sciences. The main approaches employed are primal and mixed finite element method (FEM), h version of the boundary element method (BEM), discontinuous Galerkin methods (DGM), combination of FEM, BEM, and DGM, Lagrange multiplier techniques, stabilized and enriched methods, domain decomposition methods, least squares methods, and finite volume methods. Applications include potential theory, electromagnetism, elasticity, fluid mechanics, fluid-solid interactions, acoustics, hyperbolic conservation laws, oceanography, and environmental flows.
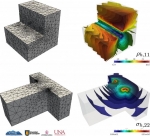
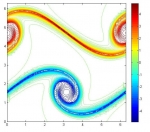
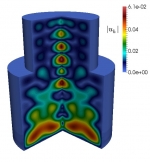
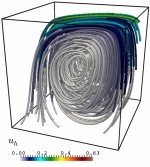
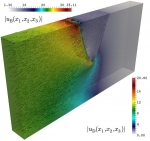
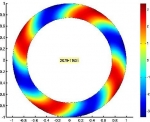
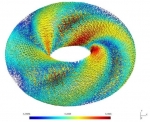
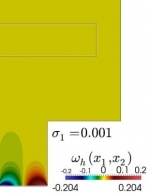
In particular, during recent years, the following specific topics have been considered: mathematical modeling and numerical simulation of vibrations in coupled systems consisting of elastic structures interacting with compressible fluids; mathematical and numerical analysis of mixed variational formulations for linear and nonlinear transmission problems on interior and exterior domains in particular mixed finte element methods for several type of fluid-solid interaction problems; analysis of efficient finite element methods to solve Maxwell equations in the low frequency regime; a-posteriori error analysis to control the discretization errors, and adaptive algorithms to automatically generate efficient ansatz spaces; efficient solution procedures for the arising discrete systems, including algorithms and analysis of preconditioners; high order boundary element methods to efficiently approximate the unknowns associated with the boundary integral operators; numerical analysis of non-linear hyperbolic equations with relaxation terms and application to chromatography and distillation models; parameter identification of parabolic degenerated equations modeling sedimentation problems; mathematical modeling of traffic flow using conservation laws and hyperbolic equations; modeling of pollutant dispersion and degradation in aquatic media. Some illustrations of the above are displayed in the following gallery of examples: