Análisis Numérico de Ecuaciones Diferenciales Parciales
El Análisis Numérico es una de las pocas ramas que están presentes en casi todas las áreas de Matemáticas Aplicadas. De hecho, los beneficios del Análisis Numérico tienen un impacto en muchas áreas de las Matemáticas y las Ciencias Aplicadas, tales como la ingeniería, la física y los sectores público y privado (industria minera, ecología, sector salud, industria de la celulosa y papel, educación). El Grupo de Investigación en Análisis Numérico de Ecuaciones Diferenciales Parciales de CI²MA, actualmente formado por 13 investigadores, se centra en el análisis matemático y numérico de varios problemas de límites lineales y no lineales y de valores iniciales que aparecen en las ciencias físicas y en la ingeniería. Los principales enfoques utilizados son el método de elementos finitos primarios y mixtos (FEM), la versión H del método de elementos límite (BEM), los métodos Galerkin discontinuos (DGM), la combinación de FEM, BEM y DGM, las técnicas multiplicadoras de Lagrange, los métodos estabilizados y enriquecidos, métodos de descomposición de dominios, métodos de mínimos cuadrados y métodos de volumen finito. Las aplicaciones incluyen teoría potencial, electromagnetismo, elasticidad, mecánica de fluidos, interacciones fluido-sólidas, acústica, leyes de conservación hiperbólica, oceanografía y flujos ambientales.
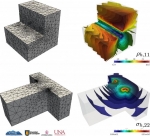
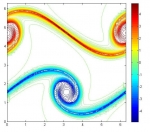
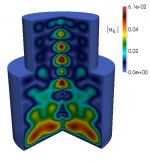
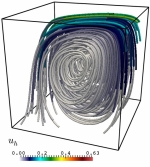
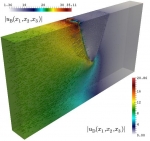
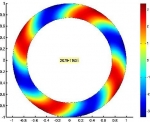
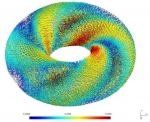
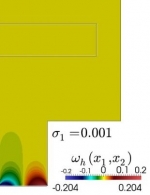
Particularmente, durante los últimos años se ha investigado los siguientes temas específicos: modelización matemática y simulación numérica de vibraciones en sistemas acoplados consistentes en estructuras elásticas que interactúan con fluidos compresibles; Análisis matemático y numérico de formulaciones variacionales mixtas para problemas de transmisión lineal y no lineal en dominios interiores y exteriores en particular métodos mixtos de elementos finitos para varios tipos de problemas de interacción fluido-sólido; Análisis de métodos eficientes de elementos finitos para resolver ecuaciones de Maxwell en el régimen de baja frecuencia; Análisis de errores a-posteriori para controlar los errores de discretización, y algoritmos adaptativos para generar automáticamente espacios ansatz eficientes; Procedimientos de solución eficientes para los sistemas discretos que surgen, incluyendo algoritmos y análisis de precondicionadores; Métodos de elemento de límite de orden alto para aproximar eficientemente las incógnitas asociadas con los operadores de la integral de frontera; Análisis numérico de ecuaciones hiperbólicas no lineales con términos de relajación y aplicación a modelos de cromatografía y destilación; Identificación de parámetros de ecuaciones degeneradas parabólicas que modelan problemas de sedimentación; Modelización matemática del flujo de tráfico utilizando leyes de conservación y ecuaciones hiperbólicas; Modelización de la dispersión y degradación de contaminantes en medios acuáticos. Algunas ilustraciones de lo anterior se muestran en la siguiente galería de ejemplos: